Bitcoin’s network congestion can vary wildly. During some hours of some days, tens of thousands of transactions are waiting to get included in a block, causing fees to spike and leaving many users waiting. During slower hours, meanwhile, there aren’t even enough transactions to fill all blocks, and the smallest of fees suffice for quick confirmation.
Network congestion during peak hours is of course a big problem for services that need to make many transactions, fast. Exchanges, mining pools or payroll services, for example, sometimes pay hundreds of users simultaneously — and these users may be understandably impatient to get their money. The services therefore pay high fees, bumping all other transactions on the Bitcoin network back in the queue.
Now, Bitcoin Core contributor Jeremy Rubin believes he has figured out how to reliably smooth out network congestion, increasing Bitcoin’s throughput during peak hours.
His proposal is called OP_SECURETHEBAG.
Securing the Bag
To understand OP_SECURETHEBAG (which, from now on, we’ll simply call “Secure the Bag”), let’s take a practical example and start from the basics. In this example, 12 customers all request that an exchange issue their withdrawals while fees are high. (In reality this might easily be 1,200 customers — but with 12, the concept is easier to explain.)
Even without Secure the Bag, the exchange is sensible and does not create 12 separate transactions to pay each customer individually. Instead, to save on fees, it creates a “batched” transaction, which is more compact. The transaction consists of, say, three inputs (referring to the “from” addresses, all three of which belong to the exchange) and 12 outputs (which include the “to” addresses, belonging to the different customers). In this example, the amounts add up nicely, so there is no change address.
In the images below, the transaction would look like transaction A on the right — not like 12 individual transactions as shown to the left.
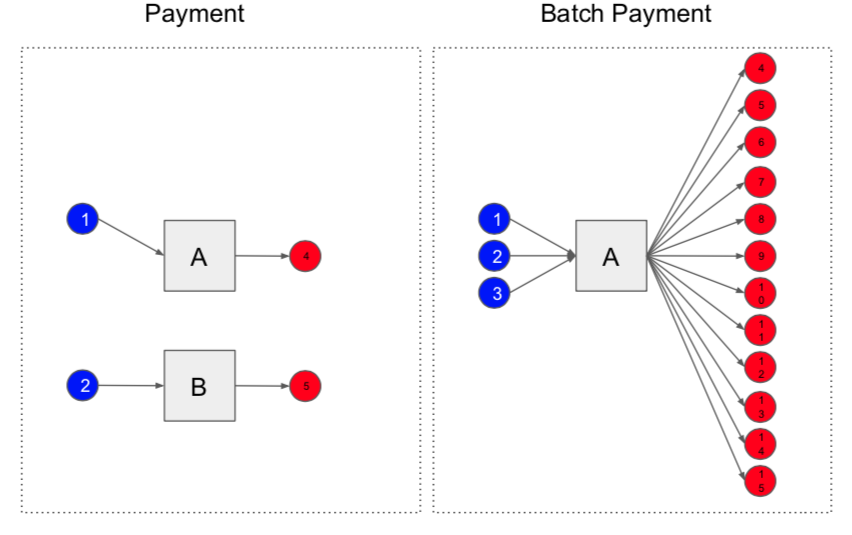
Because the batched transaction includes so many outputs — one for each customer — it is quite large, data-wise. The larger a transaction is, the more it costs to have it included in a block. And during peak hours, it will be quite expensive for the exchange to have the transaction confirm quickly. (Not as expensive as 12 individual transactions would be, but still expensive.)
Now, it is possible for the exchange to include a lower fee instead, in which case it would just take a while for the transaction to confirm. But until it confirms, customers would be waiting for their money, unsure if they will really receive it at all: The money could be double-spent until the transaction is included in a block. This leaves the customers unhappy, and the exchange doesn’t want that. (In some cases, it may not even be an option to let customers wait: Payroll services could, for example, be contractually obligated to have the transaction confirmed on a particular day.)
This is where Secure the Bag comes in.
Secure the Bag is a proposed “OpCode”: an addition to Bitcoin’s programming language. This OpCode would essentially let the exchange “split” its batched transaction into two transactions: a “sending” and “receiving” transaction.
The first of these — the “sending” transaction — includes the three original inputs, referring to the addresses owned by the exchange. But it includes only one special output. This output is called a “committed output” and contains a special cryptographic hash: a seemingly random but relatively short string of numbers.
This hash essentially serves as a unique serial number, linking it to the other of the two transactions: the “receiving” transaction. Key to Secure the Bag, the only way the committed output can be spent is through this specific “receiving” transaction, to which it is linked through the hash. (In technical terms, the hash commits to the entire “receiving” transaction except for the “prevouts,” but this is an implementation detail.)
The “receiving” transaction, then, can be considered the second half of the original transaction. It contains only one input, referring to the committed output from the “sending” transaction, and all the 12 outputs. This “receiving” transaction, with all the outputs, is therefore much larger than the “sending” transaction.
In the images below, you can see the normal batched transaction on the left, and the two separated transactions (“sending” and “receiving”) of a Secure the Bag payment on the right.
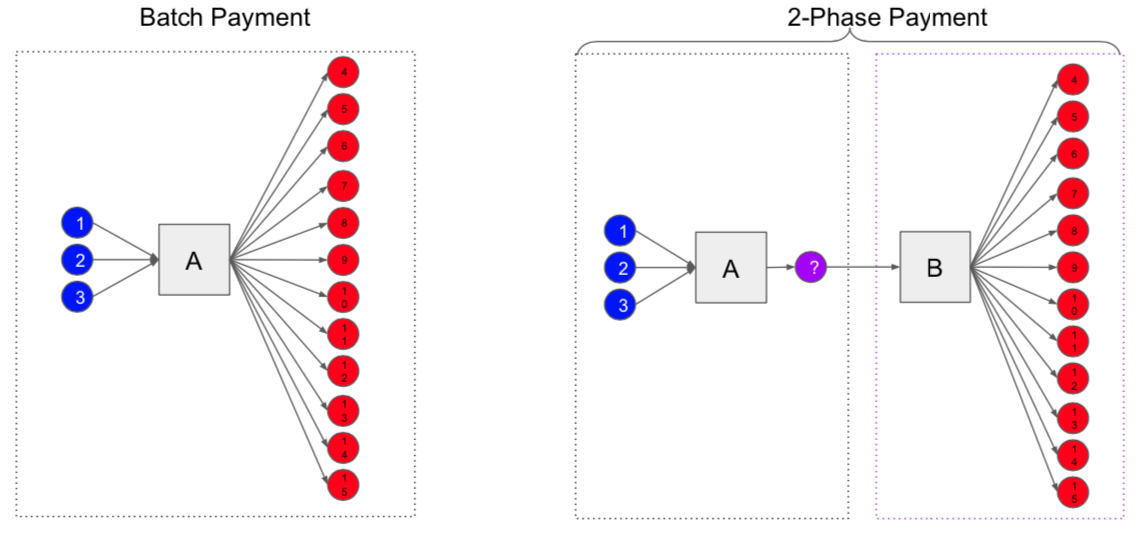
As it issues the withdrawal to its 12 customers, the exchange broadcasts both the “sending” and “receiving” transactions. But there is one big difference between the two, and this is the heart of the trick. The smaller “sending” transaction includes a relatively large fee, to ensure that it confirms fast. Since this transaction is small, data-wise, even a relatively large fee is manageable. The larger “receiving” transaction, in contrast, includes a much lower fee, meaning it could take a while for the exchange to confirm it.
The larger “receiving” transaction, in contrast, includes a much lower fee, meaning it could take a while to confirm. But this time, the wait for a low-fee transaction to confirm shouldn’t be a big problem for the customers, because once the “sending” transaction has confirmed, it ensures that all the money is guaranteed to the “receiving” transaction. The funds are anchored in the blockchain and have nowhere else to go but to the exchange’s customers.
The money isn’t quite there yet … but the bag has been secured.
Child Pays for Parent
While the basic example as outlined above would ensure* that the exchange’s 12 customers get their funds eventually, this may not satisfy all of them quite yet.
(*In the event that transaction fees never come down to the required level, the “receiving” transaction would actually not confirm on its own; this is resolved though the same trick, as explained in the remainder of this article.)
By way of example, Alice, one of the 12 customers, must pay her landlord today. Therefore, just knowing that she will receive her money eventually doesn’t suffice — no matter how sure she is that she will indeed receive it. She actually needs to be able to spend her output.
This is technically possible. Alice can take her unconfirmed output (one of the 12), and spend it in a new transaction immediately. The only problem: Alice’s transaction will only confirm after the “receiving” transaction is also confirmed. Meanwhile her landlord is demanding a confirmed transaction today.
Luckily enough, Alice can leverage an older Bitcoin trick to ensure that both the “receiving” transaction and her own transaction confirm: “Child Pays for Parent” (CPFP). Basically, if Alice includes a high enough fee in her transaction to the landlord, miners will be incentivized to include the “receiving” transaction in a block as well — even if they don’t care for the fee on the “receiving” transaction itself. After all, they only get Alice’s high fee by confirming both.
That said, compensating for the large “receiving” transaction would be quite expensive. That’s why the exchange used Secure the Bag in the first place. Instead of the exchange, now Alice would be paying for the batched transaction to all 12 customers. This wouldn’t make her a very happy customer.
Fortunately, Secure the Bag offers a better solution.
Tree Payments
To solve Alice’s problem, the exchange could take the Secure the Bag trick one step further.
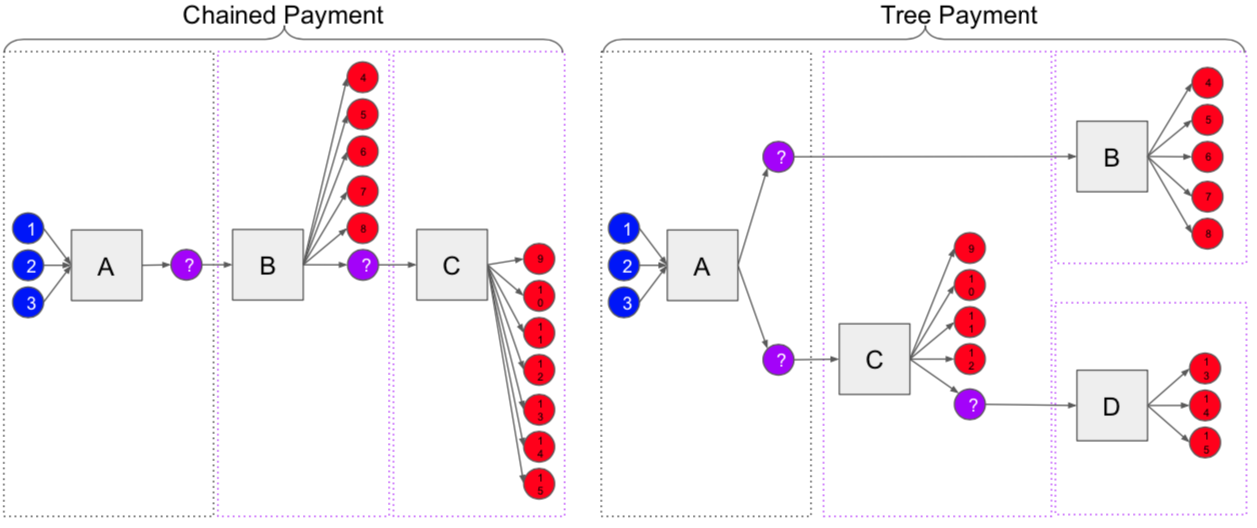
In the basic example shown above, the “sending” transaction includes one Secure the Bag output, while a single “receiving” transaction includes one corresponding Secure the Bag input and 12 normal outputs. But it is possible to further split up these 12 outputs over more “receiving” transactions.
The “sending” transaction could, for example, include two Secure the Bag outputs, referring to two different “receiving” transactions that each include six normal outputs. This would mean, of course, that the “sending” transaction is a bit more expensive to have confirmed fast, but Alice’s cost would be more than halved: She’d now pay for only five other customers instead of eleven.
Even better, the exchange could create “intermediate” transactions between the initial “sending” transaction and the eventual “receiving” transactions! These “intermediate” transactions would all include one Secure the Bag input and one or several Secure the Bag outputs and possibly normal outputs, creating a tree structure. In this way, the exchange can reasonably minimize the CPFP cost, even for customers who need to spend their funds straight away. Customers in a hurry would need to pay for the intermediate transactions relevant to them, at most, and ignore the rest.
As shown in the images below, the exchange can create such a tree as creatively as desired, depending on what works best for its customers. (More intermediate steps would generally require more total transaction data to be confirmed on the blockchain — but less cost per individual user. “Chained” payments are similar to Tree payments, but are more dependant on the chronology of transactions.)
Details and Deployment
This article describes fairly basic implementations of Secure the Bag. In actuality, the proposal could be implemented and utilized in various ways. For example, rather than Alice needing to use CPFP to be able to pay her landlord, she could receive funds into Lightning channels and instantly be able to pay her landlord through those. There are also other, more complicated solutions to speed up the “receiving” transaction.
Also, the proposed Secure the Bag OpCode is, strictly speaking, not the only way to realize the two-phase payment solution. Even with the current Bitcoin protocol, something similar could be achieved — but it would require all recipients to coordinate and cooperate, which is not very likely in the example of an exchange and its customers, and such a scenario would become harder as more users join. Others solutions (such as covenants) would require Bitcoin protocol upgrades.
Secure the Bag, too, would require a protocol upgrade by means of a backward-compatible soft fork. Rubin has already done most of the coding work required — though both the code and the idea are still subject to review. Further, even if the proposal passes all peer review, protocol upgrades can take a while to be adopted. As such, there is currently no estimation as to when Secure the Bag will be live on Bitcoin — if ever.
Thanks to Jeremy Rubin for information and feedback. For more information, simulation data and various other use cases for Secure the Bag, also see the relevant Bitcoin Improvement Proposal, the development mailing-list discussion on the topic and Rubin’s full presentation at Scaling Bitcoin 2019 in Tel Aviv:
The post Secure the Bag: Cutting Transactions in Half to Resolve Bitcoin Network Congestion appeared first on Bitcoin Magazine.
Via: Secure the Bag: Cutting Transactions in Half to Resolve Bitcoin Network Congestion
A Blockchain is a growing list of records, called blocks, which are linked using cryptography. Cryptography is the practice and study of techniques for secure communication in the presence of third party adversaries. Cryptocurrency is a digital currency that uses encryption (cryptography) to regulate the generation of currency and verify the transfer of funds, independently of a central bank.
Blockchain 101 · Crytpo Currency Market
---------------------------------------------------
Trezor: Hardware Wallet
Binance: Exchange for Traders
Ledger Nano S: Hardware Wallet
Coinbase: Exchange for Investors
CoinSwitch: Wallet-to-Wallet Exchange
